Gerbang Logika adalah rangkaian dasar yang membentuk komputer. Jutaan
transistor di dalam mikroprosesor membentuk ribuan gerbang logika.
Sebuah gerbang logika sederhana mempunyai satu terminal output dan satu
atau lebih terminal input.
Keluarannya dapat tinggi (1) atau rendah (0), tergantung level digital yang diberikan pada terminal input. Gerbang logika sangat penting dipakai dalam berbagai rangkaian elektronika.
Berikut 3 gerbang logika yang diantaranya OR, AND dan NOT Inverter.
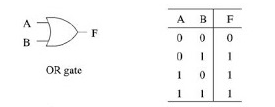
1. GERBANG OR
Gerbang OR adalah gerbang yang akan memberikan keluaran berlogika 1
bila gerbang inputnya ada yang diberikan logika 1. Gerbang OR juga bisa
mempunyai lebih dari 2 input. Dalam persamaan Boolean dapat ditulis X =
A + B
2. GERBANG AND
Gerbang AND adalah gerbang yang memberikan keluaran 1 bila semua
masukkan diberikan 1. Pada gambar tabel kebenaran untuk 2 buah masukkan
pada gerbang AND, dengan X akan berlogika 1 jika kedua input berlogika
1. Dalam persamaan Boolean dapat ditulis X=A.B
3. GERBANG NOT (Inverter)
Gerbang logika inverter digunakan seperti gerbang logika AND dan OR
terkecuali gerbang inverter mempunyai tambahan rangkaian output yang
membalik. Pada dasarnya ada tiga gerbang logika inverter : NAND
(NOT-AND) dan NOR (NOT-OR). Jika inverter ini dimasukkan 1 akan mengubah
keluaran inverter menjadi 0 daan jika inverter ini dimasukkan 0, maka
akan mengubah keluaran inverter menjadi 1. Persamaan Boolean untuk
inverter adalah  ( X = Tidak A).
( X = Tidak A).
Contoh Soalnya :
1. Z = A + ( B . C )
Tabelnya
:
A
|
B
|
C
|
B
. C
|
A ( B . C )
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
2.
Z = ( A + B ) . C
Tabelnya
:
A
|
B
|
C
|
A
+ B
|
( A + B ) . C
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
3.
Z = ( A + B ) . À
Tabelnya
:
A
|
B
|
A
+ B
|
( A + B ) . À
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
Tabelnya
:
A
|
B
|
A . B
|
( A . B ) + B
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
Terima kasih telah mengunjungi situs elfanteen.blogspot.co.id semoga bisa bermanfaat dan menambah pengetahuan atau wawasan, dan juga jangan lupa like facebook kami, terima kasih :)
Silahkan komen kalao tidak mengerti...